<!–
title: 力学
date: 2024-09-08 16:57:51
tags:
— -->
前言
从高中的时候就一直想总结一下,但苦于没有时间。
现在有时间了,顺便用用markdown,总结一下脑子里的物理知识有哪些(~ ̄▽ ̄)~
顺便稍稍复习一下下学期即将开课的大物I
二编:寒假的时候略无聊,心血来潮想写写的笔记,幻想着能复习一下大物I,可惜这学期太忙了根本没听课(误)。(放在这里做下测试吧)下学期大物II提前上完了,不过还有固体物理,后面应该会更新笔记的
————————哎,为数不多的物理课了…(心向物理bushi)
力学
一、运动的描述(运动学):
Describe objects:
1.位置:位置矢量r
2.速度:速度矢量v= dtdrr
3.加速度:a= dtdvv
(一)对于同一参考系下不同“视角”的描述
坐标系下的描述
1.任意曲线坐标系:u,v,w
对于其坐标下物体的小位移,对应r矢量小位移drr,有
drr=∂u∂rrdu+∂v∂rrdv+∂w∂rrdw
实例:
1.直角坐标系:
drr=∂x∂rrdx+∂y∂rrdy+∂z∂rrdz
其中由几何运算:
∂x∂rr即为沿x轴方向单位矢量x^x^
∂y∂rr即为沿y轴方向单位矢量y^y^
∂z∂rr即为沿z轴方向单位矢量z^z^
亦即drr=x^x^dx+y^y^dy+z^z^d
速度
vv=dtdrr=dtdxx^x^+dtdyy^y^+dtdzz^z^
=x˙x^x^+y˙y^y^+z˙z^z^
加速度
aa=dtdvv=x¨x^x^+y¨y^y^+z¨z^z^
PS:(由于直角坐标的单位正交基不是 位置or时间 的函数,在其坐标下的导数就 等于 对应分量导数的矢量和)
2.柱坐标系:
drr=∂ρ∂rrdρ+∂θ∂rrdθ+∂z∂rrdz
其中由几何运算:
∂ρ∂rr为沿ρ方向单位矢量ρρ^
∂θ∂rr为ρθθ^,其中θθ^为沿θθ方向(切向)单位矢量
∂z∂rr即为沿z轴方向单位矢量x^x^
亦即drr=dρρρ^+ρdθθθ^+dzz^z^
速度
vv=dtdrr=ρ˙ρ^ρ^+ρθ˙θ^θ^+z˙z^z^
加速度
aa=dtdvv=ρ¨ρ^ρ^+ρ˙dtdρ^ρ^+ρ˙θ˙θ^θ^+ρ˙θ¨θ^θ^+ρθ˙dtdθ^θ^+z¨z^z^
其中dtdρ^ρ^和dtdθ^θ^怎么处理⟶利用全微分处理,dρ^ρ^和dθ^θ^对坐标的全微分是可以获得的:
dρ^ρ^=∂ρ∂ρ^ρ^dρ+∂θ∂ρ^ρ^dθ=0+dθ⋅θ^θ^dθ^θ^=∂ρ∂θ^θ^dρ+∂θ∂θ^θ^dθ=dρ⋅(−ρ^ρ^)=−dρ⋅ρ^ρ^
因此
dtdρ^ρ^=θ˙θ^θ^dtdθ^θ^=−ρ˙ρ^ρ^
aa=dtdvv=(ρ¨−ρθ˙2)ρ^ρ^+(2ρ˙θ˙+ρθ¨)θ^θ^+z¨z^z^
3.球坐标系,推导方式类似,这里直接给出结果
aa=balabala...(手动狗头bushi)
4.平面极坐标(直接由柱坐标系退化即可)
aa=dtdvv=(ρ¨−ρθ˙2)ρ^ρ^+(2ρ˙θ˙+ρθ¨)θ^θ^
2.自然坐标系
自然坐标系的运动的描述:
⟶把运动分解为直线运动和圆周运动
其本质是对于速度矢量的大小和方向进行度量

这里其实用到了一个思想⟶将时间项dt利用其他不显含时间的量ωω来进行表示
这与有心力场中轨道微分方程 Binet公式的思想相同
沿运动方向:切向加速度
垂直运动方向:向心加速度
合并在一个式子里即aa=ρv2r^r^+s¨τ^τ^
另外的应用——软绳坐标(在约束中再提)
(二)对于不同参照系下同一“视角下的描述”
参考系
相对于任意参考系,空间是非均匀且各向异性的,即某个物体与其他物体没有相互作用,它在空间中的不同位置和不同指向在力学意义上是不等价的.同样,一般情况下任意参考系中的时间也是非均匀的,即不同时刻也是不等价的.显然,时间和空间的这些性质使力学现象的描述变得复杂.
然而,似乎总是存在某种参考系,空间相对它是均匀的、各向同性的,时间相对于它是均匀的——这样的参考系称为惯性参考系。
————上述两段摘自Landau力学
伽利略变换
对于两个惯性参考系之间的变换,
r′r′=rr+uut
t′=t
两个式子即代表了两个惯性参照系的坐标与时间关系,后者为经典力学中的绝对时间假设
对上式进行求导,得到了两个坐标系的速度变换公式
v′v′=vv+uu
伽利略相对性原理也可以表述为:力学运动方程在伽利略变换下具有不变性(形式不变)
在不同坐标系下描述物体的运动
1.两个互作平动的参照系之间的变换
互作平动,但是未必相对运动是匀速运动r′r′=rr+uut ✘
下面给出变换公式及其推导
r′r′=rr+ρρ
dtdρρ≜uu,dtdrr≜vv,dtdr′r′≜v′v′,dtduu≜AA
s.t.v′v′=vv+uu
a′a′=aa+AA
其中物理量含义不做过多解释;
2.两个互作转动的参照系之间的变换
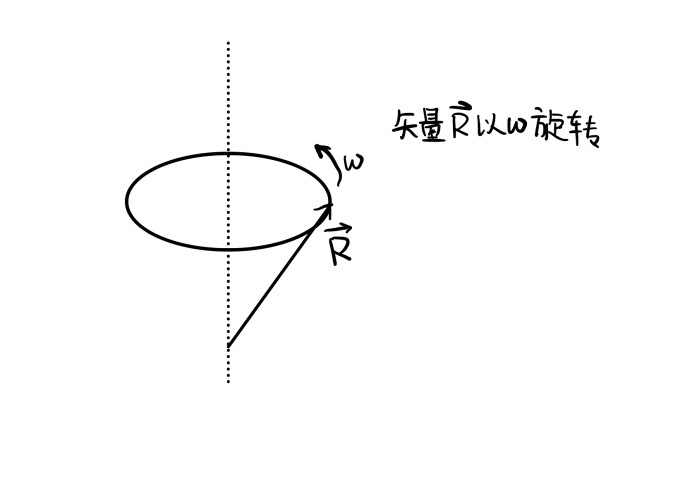
在参考系(S)内,如果RR矢量绕某个轴以角速度ωω转动(注意方向是沿轴向上不是逆时针),
则对RR矢量求导满足(记以角速度ω转动的参考系为S’)
(dtdRR)S=(dtdRR)S′+ωω×RR
其中(dtdRR)S′实际为RR矢量在S’系中不旋转,只伸长or缩小
应用上述结论,则有速度变换
(dtdrr)S=(dtdrr)S′+ωω×rr
即v′v′=vv+ωω×rr
再求导
(dtdv′v′)S=(dtd(vv+ωω×rr))S=(dtdvv)S+(dtd(ωω×rr))S
=(dtdvv)S+(dtdωω)S×rr+ωω×(dtdrr)S
=(dtdvv)S+ββ×rr+ωω×(dtdrr)S
而我们又知道(dtdrr)S=v′v′=vv+ωω×rrand(dtdvv)S=(dtdrr)S′+ωω×vv
s.t.(dtdv′v′)S==(dtdvv)S+ββ×rr+ωω×(vv+ωω×rr)
=(dtdrr)S′+ωω×vv+ββ×rr+ωω×(vv+ωω×rr)
=(dtdrr)S′+2ωω×vv+ββ×rr+ωω×(ωω×rr)
(dtdv′v′)S≜a′a′(dtdvv)S′≜a′a′
s.t.a′a′=aa+2ωω×vv+ββ×rr+ωω×(ωω×rr)
此即两个互作转动的参照系之间的加速度变换(累死了(´〜`*) )
前情提要:
上面对于运动的描述都是对于单个物体(质点)而言,对于质点系而言,当然可以对每个质点单独进行描述,但是对于质点之间,存在着一定的约束,下面我们讨论有约束关系我们能获得什么:
(三)约束
理想约束/非理想约束,这个等到后面分析力学再详细展开(或者再这里再补充)
这里仅举常用的一些例子,但是会从更数学的角度去处理约束关系,和从物理的角度对比一下,更好的理解运动关联的那些事
eg1:杆模型
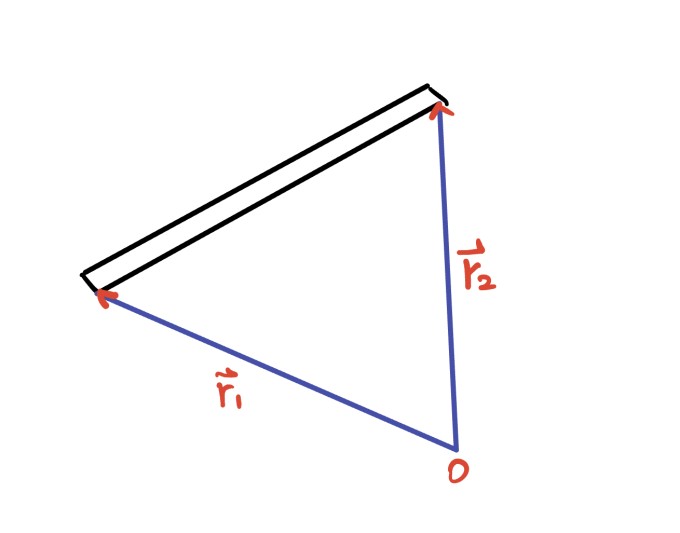
杆模型这里只关注两个端点的约束关系,杆长为l,选取一个原点为O,则此时描述两个质点的运动由r1r2r1r2来决定
那这两个质点(两个端点)有什么约束关系——很简单,∣r1r1−r2r2∣=l
但是操作起来不是那么方便,于是上式改写为(r1r1−r2r2)2=l2
这样写有什么好处——可以求导了!式子两边对时间求导
dtd(r1r1−r2r2)2=dtd{(r1r1−r2r2)⋅(r1r1−r2r2)}
=(r1r1−r2r2)⋅(v1v1−v2v2)+(v1v1−v2v2)⋅(r1r1−r2r2)
=2(r1r1−r2r2)⋅(v1v1−v2v2)
=dtd(l2)=0
由此我们获得了一个信息——(r1r1−r2r2)⋅(v1v1−v2v2)=00
这句话代表了什么⟶r1r1−r2r2记为ll
上式化为ll⋅v1v1=ll⋅v2v2
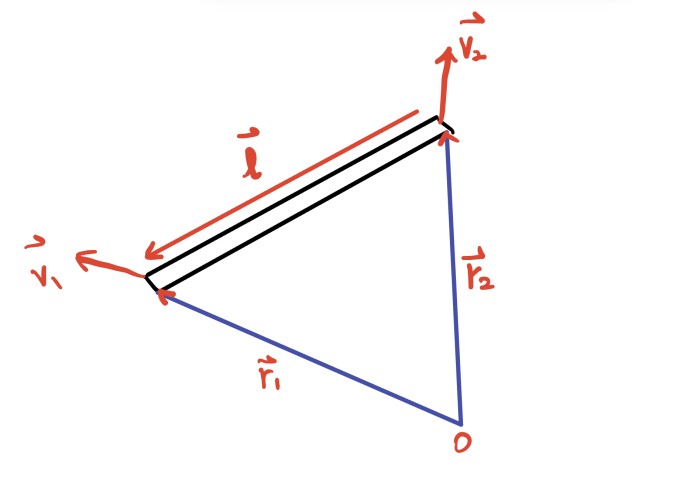
再图里面看是不是就很明显,ll⋅v1v1=ll⋅v2v2意思就是沿杆的方向速度相等(图片中两个速度显然不符合实际情况)
————显然是废话{bushi}
从这里面其实我们就能更加深刻的理解,平时我们所说的沿杆的方向速度相等的更深层次的原理,而不是一些物理直觉(当然直觉也是有理有据的)
我们再看r1r1−r2r2=ll这个式子,在平面中,ll往往是以平动加转动的方式在“运动”,那么我们尝试对ll进行求导,
显然,这和上面旋转坐标系那里提及的求导方式是一致的,
dtdll=对长度的求导+对方向的求导
=00+ωω×ll
=ωω×ll
也就是说对r1r1−r2r2=ll两边求导,会得到——
v1v1−v2v2=ωω×ll
这个式子我们再看,它有用了起来
v1v1−v2v2=ωω×ll 其实就是以一个端点为参考系,另一个端点必然是绕原来的端点(在系中静止的)圆周运动
再求导可以得到
a1a1−a2a2=dtd(ωω×ll)=ββ×ll+ωω×dtdll=ββ×ll+ωω×(ωω×ll)
即,由一个简单的杆约束方程,我们得到了如下信息
ll⋅v1v1=ll⋅v2v2
v1v1−v2v2=ωω×ll
a1a1−a2a2=ββ×ll+ωω×(ωω×ll)
eg2:软绳模型——既然前面的情形很常见,那么接下来讨论一个稍微不常见的软绳模型








